意外と簡単！２桁の掛け算を暗算で素早く解く裏ワザ

　２桁の掛け算は、多くの人にとって頭を悩ませる計算ですが、もしそれを暗算で素早く解けるようになれば、周りからの評価も一気にアップするはずです。

　実は、掛け算には規則性があり、そのパターンを覚えれば、２桁の計算も難しくありません。

　今回の記事では、簡単にマスターできる２桁の掛け算のコツを「６パターン」紹介します。暗算が得意になれば、日常生活でも一目置かれる存在に！

そもそもなぜ学校で教えない？
２桁の掛け算を暗算で素早く解く方法
さいごに

そもそもなぜ学校で教えない？

　そもそも、なぜ学校では２桁の掛け算を暗算で教えないのでしょうか？

　２桁の掛け算自体は小学校低学年で習いますが、そこで教わるのは伝統的な筆算の方法です。しかし、このやり方は手間がかかり、時間もかかるため、面倒だと感じる人も多いでしょう。

　では、なぜ効率的な暗算のテクニックが学校で教えられないのか？

　その理由は、筆算があくまで基本の計算方法であり、応用力を高めるために不可欠だからです。

　また、基礎がまだしっかりしていない段階で、裏技的な方法を教えると混乱を招く可能性があるため、学校教育では避けられているのです。

２桁の掛け算を暗算で素早く解く方法

方法1：「２乗の計算」は、おみやげ暗算法で簡単に暗算できる

　２乗の計算は、暗算の中でも非常に計算しやすいと有名です。その１つとして、おみやげ暗算法をご紹介します。

　２桁の２乗の計算と言えば、３３×３３、６９×６９、７２×７２のように、暗算が難しいように思えます。

　計算の流れは、掛け算に使う数字の１桁目を、「０」にして計算しやすく形を変えます。１桁目の数字を、足し引きし、０にします。

　15×15の計算を例に説明します。１桁目の5を移動して計算することができます。

　どういうことかと言いますと、「15×15」を「10×20」に変換します。

　10×20＝200です。計算しやすくなりました。

　これに、さきほど移動した5の２乗を足すだけで、なんと答えが出てくるのです。

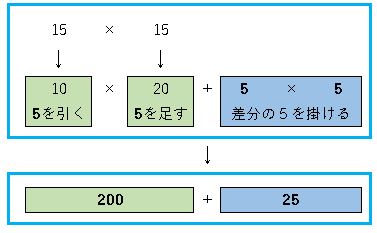
　15×15　＝　10×20　＋　5×5　＝　225　という表記になります。

　他にも例をあげてみます。

45×45
＝50×40＋5×5
＝2025 　(5を移動)
77×77
＝74×80＋3×3
=5929 　(3を移動)
22×22
＝24×20＋2×2
＝484 　(2を移動)
31×31
＝32×30＋1×1
＝961 　(1を移動)

　計算の中で０が増えるだけで、一気に計算しやすくなります。

　1桁目が「5の場合」は、特に計算しやすいです。10の倍数の掛け算に25を足すだけです。

15×15
＝10×20＋25
＝225
25×25
＝20×30＋25
＝625
35×35
＝30×40＋25
＝1225
65×65
＝60×70＋25
＝4225
95×95
＝90×100＋25
＝9025

　１桁目の移動が１～３の場合は、1×１、２×２、３×３なので、繰り上がりがありませんので計算しやすくなります。

19×19
=18×20+1×1
=360+1
=361
18×18
=16×20+2×2
=320+4
=324
17×17
=14×20+3×3
=280+9
=289

　2桁の２乗の計算のみに使えるワザですが、覚えたら早いです。

　よく見てみると、１桁目を移動するのが、１～５の５パターンしかありません。

方法2：「因数分解」でラクラク暗算

　掛け算の暗算をするときに、０が増えるだけで、計算しやすくなると書きました。

　たとえば20×20は？と聞かれたら、ほとんどの方が、400とすぐに答えられるでしょう。

　では1つ数字をずらしてみるといかがでしょうか？、19×21はどうでしょうか？暗算できますか？

　実は、19×21とは、非常に計算しやすい数字なのです。高校の数学を学んだことがある方は、因数分解を習ったことがあると思います。

公式:(ｘ＋1)×(ｘ－1)＝ｘ(２乗)－1

　さきほどの19×21を、因数分解を使って、計算しやすくしてみます。

　そうすると、(20＋1)(20－1)となり、20(2乗)－1で計算できることになります。ここまで変換できれば、答えは簡単ですね。400-1となり、399が答えになります。

　他にもいくつか例を挙げてみます。

38×42
＝(40－2)(40＋2)
＝1600－4
＝1596
27×33
＝(30－3)(30＋3)
＝900－9
＝891
44×56
＝(50－6)(50＋6)
＝2500－36
＝2464

　方法２で紹介した「おみやげ暗算法」を併用すると、ちょっと難しい計算も、あっという間に暗算ができてしまう形もあります。

　たとえば、44×46です。因数分解を使って(45－1)(45＋1)に置き換えてみます。

　45×45－1となりました。”45×45”の部分は、おみやげ暗算法を使って2025と解けますので、あとは－1をして2024という答えが出てきます。

　ちなみに、因数分解を使う暗算は、２桁に限らず、３桁４桁でも計算しやすい場合があります。例えば以下のような場合です。

299×301
＝(300－1)(300＋1)
＝90000－1
＝89999
402×398
＝(400－2)(400＋2)
＝160000－4
＝159996

方法3：あとで倍するだけの暗算

　２桁同士の暗算が、難しいなら、分解して１桁に形を変えた方が計算しやすくなる場合があります。細かく分解し、後で元に戻して計算する方法です。

　16×14という比較的小さな数字の計算ならば、分解して計算したほうが暗算しやすい場合があります。

16×14
＝(8×2)×(7×2)
＝8×7×2×2に並び替えます。

　8×7は、56と簡単に出てきます。あとはこの56という数字に、×2を2回するだけで解けちゃいます。

　掛け算が苦手な人でも、頭の中で、用意された数字を倍にするだけというのは、比較的簡単なことです。

　56⇒112⇒224とあっというまに、答えが出てきました。

　18×22の場合はどうでしょうか。

18×22
＝(9×2)×(11×2) 分解
＝9×11×2×2　並べ替え
＝99×2×2
＝198×2　　倍！
＝396　　　倍！

　「１日は、何分あるでしょうか？」という問題があったとすれば、60分×24時間(6×2×2)と置き換えて、360分⇒720分⇒1440分となり、暗算しやすくなります。

　2倍するというのは、頭の中で計算しやすいのです。

方法4：偶数×５の倍数

　偶数と５の倍数の掛け算は、場合によっては、計算がしやすいのです。今回は、１桁目が５である数字を掛ける場合について、説明していきます。

　まず、１６×１５をご覧ください。

　ぱっと見で、簡単に暗算をするのは、難しいのでは！？と思ったはずです。どこから計算してよいのか、わからないはずです。

　では、偶数１６の部分を、８×２に分解してみましょう。

　８×２×１５に変形してみました。偶数なので、「×２」を作ることができますね。この「×２」と５の倍数は、非常に相性が良いのです。

　「２×１５」は、計算すると３０になります。

＝８×２×１５　　・・・１６を８×２に分解
＝８×３０　　　　・・・２×１５を先に計算
＝２４０

　１６×１５を８×３０に形を変えるだけで、暗算しやすい数字になり、簡単に計算することができます。

　他の例をあげてみます。２２×３５を計算してみましょう。

＝２２×３５
＝１１×２×３５　　・・・２２を１１×２に分解
＝１１×７０　　　　・・・２×３５を先に計算
＝７７０

いかがでしょうか？慣れてくれば、暗算でも簡単に計算ができるはずです。

方法5：十和一等

２桁同士の数字が、ある規則的な数字の場合に限り、簡単に計算できてしまう方法をご紹介します。十和一等と呼ばれる暗算です。

十和一等の条件として、

条件１：２つの数の１０の位の数の和が１０である（十和）
条件２：２つの数の１の位が、同じ数字である（一等）

ん？どういうことなのか、わからないかと思いますので、サンプルを下記に記載します。

７２×３２　⇒　１０の位「７＋３＝１０」、１の位が共に２
６４×４４　⇒　１０の位「６＋４＝１０」、１の位が共に４
８５×２５　⇒　１０の位「８＋２＝１０」、１の位が共に５

上記の場合に限り、十和一等の暗算が使えます。十和一等の計算方法は、以下のようになります。

手順１：１０の位の数同士を掛けたものに、１の位の数字を足す。
手順２：１の位の数同士を掛ける。
手順３：手順１で出た数値を1000の位・100の位に、手順２で出た数値を10の位・1の位にセットする。

７２×３２の場合

まず手順１、１０の位の数は、「７」と「３」です。７×３＝２１です。２１に１桁目の２を足すと２３です。
次に手順２、１の位の数は、「２」と「２」です。掛けると４になります。この場合、０４とします。
最後に手順３、手順１（２３）、手順２（０４）を、合体させます。２３０４が答えになります。

慣れてくると、２つの数字を見ただけで、数秒で暗算ができてしまいます。

６４×４４の場合

手順１では、６×４に４を足して、２８です。
手順２では、４×４で１６です。
合体させて、２８１６になります。

８５×２５の場合

手順１では、８×２に５を足して、２１です。
手順２では、５×５で２５です。
合体させて、２１２５になります。

方法6：十等一和

さきほど方法5で紹介したものと類似していますが、少し形が違います。

十等一和の条件として、

条件１：２つの数の１０の位が、同じ数字である（十等）
条件２：２つの数の１の位の数の和が１０である（一和）

どのようなパターンかと言いますと、

２４×２６
４３×４７
５２×５８

方法２の十和一等と合わせて覚えると、覚えやすいです。

十等一和の計算方法は、

手順１：１０の位の数と、１０の位の数に＋１したものを掛ける。
手順２：１の位の数同士を掛ける。
手順３：手順１で出た数値を1000の位・100の位に、手順２で出た数値を10の位・1の位にセットする。

早速、計算してみましょう。

２４×２６の場合です。

手順１：１０の位は「２」です。「２」と「３（つまり２＋１）」を掛けます。
手順２：１の位の「４」と「６」を掛けます。
手順３：手順１の６、手順２の２４を合体させます。６２４と答えが出ました。

他の例の場合です。

４３×４７＝４×（４＋１）と３×７を合体させる。２０２１になります。
５２×５８＝５×（５＋１）と２×８を合体させる。３０１６になります。

３桁同士の掛け算でも通用します。

１９６×１９４の場合です。１９×（１９＋１）と６×４を合体させると、３８０２４になります。

さいごに

他にもインド式の暗算とか、やり方はいろいろあります。

普通の人ができないような計算をパパッっと暗算で答えを出してしまうと、「賢いな！」「できるな！」と印象が良いようです。今回紹介した暗算は、覚えるより慣れろなので、時間があれば、自分で問題を作って練習してみてください。一度覚えれば、一生使えます。

小学校の頃から、ひっさんだけではなく、いろんな計算方法を知っていたら、算数がもっと好きになる子も多いかもしれません。暗算に興味を持つ子もいるかもしれません。小さいお子さんがいる方は、是非こんなやり方もあるんだよ！とご家庭で教えてあげてみてくださいね。

暗算(Mental arithmetic)

２桁の掛け算を暗算で素早く解く裏ワザ　意外と簡単！仕事でも使える！